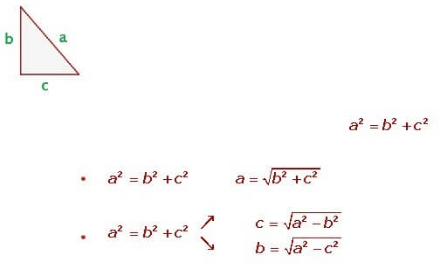Pythagorean Theorem

The Pythagorean Theorem is a fundamental relation in Euclidean geometry among the three sides of a right-angled triangle. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This theorem can be written as an equation relating the lengths of the sides a, b, and c:

Here, a² represents the length of the hypotenuse, while b² and c² represent the lengths of the triangle's other two sides.

Historical Background

The Pythagorean Theorem is named after the ancient Greek mathematician Pythagoras, who lived in the 6th century BC. Although the theorem is attributed to him, evidence suggests that the Babylonians and Indians were aware of this relationship much earlier. The theorem was known to mathematicians in the ancient civilizations of Egypt, Mesopotamia, India, and China independently of the Greek work.

Proof

There are many proofs of the Pythagorean Theorem, ranging from algebraic to geometric, some even contributed by famous personalities throughout history, including Euclid, President James A. Garfield, and Leonardo da Vinci. One of the most elegant is Euclid's geometric proof, which is found in his landmark work, "Elements".

Applications

The Pythagorean Theorem has numerous applications in various fields such as mathematics, physics, engineering, computer science, and geography. It is used in calculating distances between two points (either in a plane or in three-dimensional space), in navigation to determine the shortest path, in architecture and construction to ensure correct proportions and angles, and in computer graphics for calculating pixel distances and simulating physical phenomena.

Generalizations

The theorem has been generalized in several ways. It applies not only in Euclidean geometry but also in more complex mathematical systems such as non-Euclidean geometries, where it takes on a modified form. The concept underlying the Pythagorean Theorem also extends to higher dimensions, as seen in the law of cosines, which serves as a generalization of the theorem to non-right triangles.

In vector algebra, a version of the Pythagorean Theorem can be used to calculate the magnitude of a vector in Euclidean space, highlighting the theorem's deep and broad impact on mathematics and science.

The Pythagorean Theorem says that, in a right triangle, the hypotenuse is equal to the square root of the sum of the squares of the legs and that, in the same type of triangle, one of the legs is equal to the square root of the hypotenuse squared minus the other leg squared. But today we’re not going to worry about theory, but instead to visually see where the formula of the Pythagorean Theorem comes from.



Reference: https://teoremadepitagoras.info/formula-of-the-pythagorean-theorem/