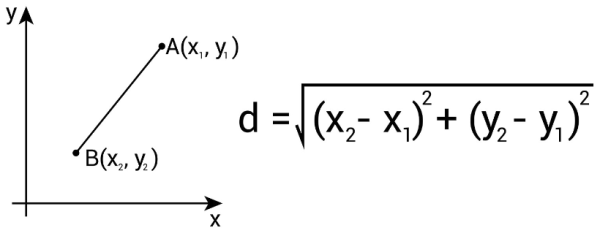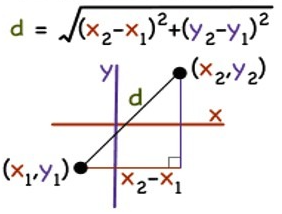Distance Formula

If the coordinate of the points A is (x1, y1) and B is (x2, y2) the formula used to calculate the distance between these two points is discussed in the image below.



Another Reference:

Have you ever found yourself marveling at the vastness of space between two points and wondered just how that distance could be measured accurately? Whether it's the few inches from your coffee cup to your laptop, the miles that stretch between cities, or even the seemingly immeasurable gaps in the cosmic tapestry, the science of measuring distance is both fascinating and fundamental. Today, we embark on a numerical journey to explore the art and science of distance measurement, a topic that finds relevance in fields ranging from everyday life to the most advanced scientific research.

What Is Distance, Anyway?

At its core, distance measures the space between two points. This concept is simple yet profound, acting as a cornerstone of both mathematics and physics. Distance can tell us how far we must travel to reach a destination, help athletes gauge the length of a race, and even allow scientists to calculate the vast expanses that separate celestial bodies.

The Mathematical Toolkit for Measuring Distance

Measuring distance requires more than just a ruler; it requires a mathematical toolkit. Here’s a breakdown of the basic tools and concepts:

The Ruler and Beyond: Units of Measurement

The most basic tool for measuring distance is the ruler, marked in units like inches, centimeters, or feet. But what about longer distances, like those between cities or planets? For these, we use units like kilometers or miles on Earth, and astronomical units (AU), light-years, or parsecs for cosmic distances.

The Coordinate System: Mapping the World

To measure distances more complex than a straight line, especially in two or three dimensions, we turn to the coordinate system. This system uses numerical values to represent points in space, making it possible to calculate the distance between any two points, whether they're on a flat plane (2D) or in space (3D).

Pythagoras Comes into Play: The Pythagorean Theorem

For distances in a two-dimensional plane, the Pythagorean theorem is our best friend. It tells us that in a right-angled triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the lengths of the other two sides. This principle allows us to calculate the straight-line distance between two points (the hypotenuse) when we know their coordinates.

Delving Deeper with Calculus

When paths become curves rather than straight lines, calculus comes to the rescue. It helps us measure the length of a curve by breaking it down into infinitesimally small straight lines and adding their lengths together. This is crucial for mapping more complex trajectories, like planetary orbits or the flight path of a drone.

Practical Applications: Distance Measurement in Real Life

Measuring distance has practical applications that touch nearly every aspect of our lives:

• Navigation and Travel: GPS technology uses the principles of distance measurement to calculate routes, using signals from satellites to triangulate positions on Earth accurately.
• Construction and Engineering: Precise distance measurement is crucial in planning and executing construction projects, ensuring structures are built correctly and fit into their designated spaces.
• Astronomy: Scientists measure vast cosmic distances to understand the universe's structure, the movement of celestial bodies, and the fundamental forces at play.

Conclusion: The Journey Continues

While we've covered some fundamental concepts and tools used in measuring distance, the journey doesn't end here. Mathematics continually evolves, offering new methods and technologies to measure distances more accurately and understand our world and the universe beyond. Whether you're a student, a professional, or just a curious mind, the exploration of distance is a mathematical adventure that stretches as far as the imagination.

As we wrap up this numerical voyage, remember that the distances between points are not just numbers; they're a testament to our quest for understanding, a measure of our curiosity, and a path to greater discoveries. So, the next time you measure the distance between two points, know that you're part of a grand mathematical tradition that spans the ages.