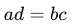| Hey there, fellow math enthusiasts! Today, we're diving deep into the world of fractions and uncovering some essential formulas that will make you the fraction master in no time. Fractions might seem like a piece of cake, but trust me, there's more to them than meets the eye. So, what exactly is a fraction? Think of it as a way to slice up numbers into smaller, more manageable pieces. A fraction consists of two integers separated by a line: the numerator on top and the denominator on the bottom. The numerator tells us how many parts we're dealing with, while the denominator tells us how many parts make up the whole. Here's why fractions are so important and why you should care about mastering them: Expressing Parts of a Whole: - Fractions are all about showing how a whole is divided into smaller parts. Whether it's dividing a pizza among friends or sharing a candy bar with siblings, fractions help us express these divisions in a clear and concise way.
Understanding Mathematical Operations: - Fractions are more than just numbers; they're a way to express division. And when it comes to math operations, fractions are your best friend. Whether you're adding, subtracting, multiplying, or dividing fractions, having a solid grasp of the formulas is crucial.
Real-World Applications: - Fractions aren't just confined to the classroom; they're used in everyday life too. From cooking recipes to measuring ingredients, from calculating finances to understanding science and engineering concepts, fractions are everywhere.
Gateway to Advanced Topics: - Understanding fractions is like unlocking a treasure trove of mathematical concepts. They form the foundation for understanding ratios, proportions, and percentages. Once you've mastered fractions, these other topics will be a piece of cake.
Now, let's break down some of the essential fraction formulas you need to know: Addition and Subtraction: - To add or subtract fractions, make sure the denominators are the same, then add or subtract the numerators. For example:
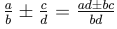
Multiplication: - To multiply fractions, simply multiply the numerators together and the denominators together. For example:
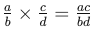
Division: - To divide fractions, multiply the first fraction by the reciprocal of the second fraction. For example:

Solving Equations: - When solving equations involving fractions, remember to find a common denominator and then simplify. For example:
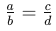 can be solved by cross-multiplying: can be solved by cross-multiplying: 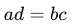
So, the next time you're faced with a fraction frenzy, remember these formulas, and you'll be slicing through those problems like a pro!

Tags: Denominator Formulas Fraction Fractions Formulas Math Formulas 분수  
|  6,869
6,869  0
0  0
0  1948
1948 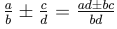
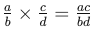

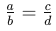 can be solved by cross-multiplying:
can be solved by cross-multiplying: