COSEC.ZIP

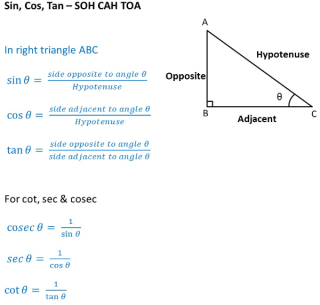
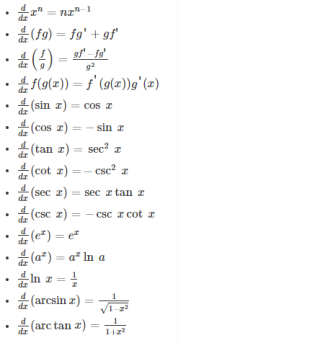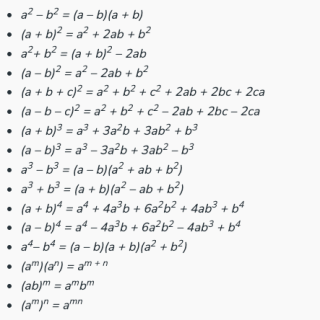Trigonometry Formulas   created at Apr 08, 2022   6,632   There are six basic functions of Trigonometry are,Sin FunctionCos FunctionTan FunctionCosec functionSec FunctionCot FunctionThe three basic trigonometric functions formulas are, Trigonometry is a branch of mathematics that studies relationships betwee...

Differential/Integral Calculus Formulas   updated at May 12, 2024   6,640   Calculus is a branch of mathematics that deals with rates of change and accumulation.It comprises two main areas: differential calculus,which focuses on rates of change and slopes of curves,and integral calculus,which deals with areas under curves and accu...

PreCalculus Formulas for Trigonometry and Math Analysis   updated at May 12, 2024   6,630   Pre-Calculus is a foundational course that prepares students for advanced mathematics.It covers two main areas: Trigonometry and Math Analysis.Understanding the key formulas and concepts in these areas is essential for success in higher-level math courses:...

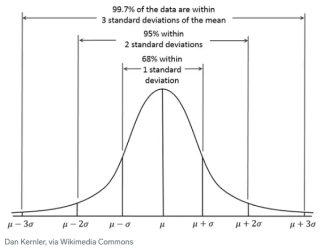
Statistics Formulas   updated at May 12, 2024   6,630   Statistics is a branch of mathematics which deals with numbers and data analysis.Statistics is the study of the collection,analysis,interpretation,presentation,and organization of data.Statistical theory defines a statistic as a function of a sample where ...

Physics Areas and Formulas   updated at May 12, 2024   6,638   Physics,the science of matter and its interactions,unlocks the mysteries of the observable universe.From the motion of celestial bodies to the behavior of subatomic particles,physics encompasses a vast array of phenomena and principles.In high school physi...

Pythagorean Theorem   created at Apr 08, 2022   6,631   The Pythagorean Theorem is a fundamental relation in Euclidean geometry among the three sides of a right-angled triangle. It states that in a right triangle, the square of the length of the hypotenuse (the side opposite the right angle) is equal to the sum...

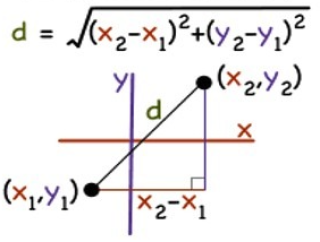
Distance Formula   created at Apr 08, 2022   6,630   If the coordinate of the points A is (x1, y1) and B is (x2, y2) the formula used to calculate the distance between these two points is discussed in the image below.Another Reference:Have you ever found yourself marveling at the vastness of space between tw...

Basic Fractions Formula   created at Apr 08, 2022   6,631   Hey there, fellow math enthusiasts! Today, we're diving deep into the world of fractions and uncovering some essential formulas that will make you the fraction master in no time. Fractions might seem like a piece of cake, but trust me, there's more to them...

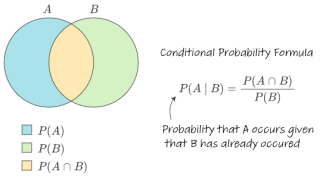
Basic Probability Formulas   updated at Sep 21, 2024   6,634   Now,I know what you might be thinking: "Probability? Sounds like a fancy word for luck." But hold on to your calculators,because probability is way more than just rolling the dice and crossing your fingers.So,what exactly is probability? Well,think of it a...

Basic Geometry Formulas in 2-D and 3-D   updated at Apr 23, 2024   6,631   Today, we're diving into the world of shapes, sizes, and dimensions with some basic geometry formulas. Now, I know geometry might not sound as flashy as algebra, but trust me, it's like the stealth ninja of mathematics. Let's explore why these formulas are...

Basic Algebra Formulas   updated at Apr 23, 2024   6,632   Hey there, fellow learners! Today, let's dive into the exciting world of basic algebra formulas. Now, I know what you might be thinking: "Algebra? Ugh, that sounds boring!" But hold your horses, because algebra is like the superhero of mathematics, and the...